Coordinate e Sistemi di riferimento¶
Un GIS è fondamentalmente un database geografico, per cui è fondamentale avere chiari i principi su cui si basano i sistemi di riferimento geografici, come sono misurate o calcolate le coordinate geografiche e come avviene la proiezione della superficie terrestre su una carta piana.
La coordinata di un punto sulla superficie terrestre è il punto di partenza della cartografia: è importante aver presente che possono esserci, per lo stesso punto, coordinate diverse, in base alle diverse modalità di calcolo.
Inoltre, visto che la Terra è approssimativamente sferica e le mappe sono piane, occorre capire anche il processo di trasformazione della superficie curva a piatta, detto proiezione geografica.
Riassumendo, le coordinate possono essere quindi distinte in:
- coordinate polari sferiche, che sono espresse in angoli di latitudine (indicata con la lettera greca
) e longitudine (
);
- coordinate cartesiane, derivanti dal processo di proiezione e espresse in metri/piedi o altre misure lineari (coordinata Est/Ovest e coordinata Nord/Sud) di distanza dall’origine.
Calcolo della coordinata di un punto¶
Per calcolare la coordinata di un punto occorre avere un sistema di riferimento rispetto al quale determinare la posizione: dal punto di vista teorico, questa operazione corrisponde alla definizione di un sistema di riferimento che fissi il numero di gradi di libertà del sistema (cioè per permetta di avere misure ripetibili).
Poiché la superficie terrestre (corpo rigido tridimensionale) ha 6 gradi di libertà si deve definire un sistema di riferimento che, «bloccando» alcune direzioni, consenta di calcolare le posizioni assolute.
Nel disegno sono mostrati i 6 gradi di libertà di un sistema tridimensionale:
- 3 di tipo traslazionale, rispetto ai 3 piani cartesiani x-y-z (indicati con 1, 2, 3);
- 3 di tipo rotazionale (indicati con 4, 5, 6).

Dal punto di vista pratico, l’uso del filo a piombo per determinare l’altezza di una stella “fissa” o del Sole, cioè l’angolo che questa forma rispetto ad uno strumento di misura (goniometro), è stato per tanto tempo (prima dell’arrivo dei satelliti) l’unico modo per avere il riferimento inerziale voluto, in grado di bloccare i gradi di libertà del sistema, mettendo il goniometro in asse con le linee del campo gravitazionale. La perpendicolarità di questo strumento permette di “bloccare” sia le traslazioni che le rotazioni, ottenendo un sistema di rifererimento utilizzabile per misure ripetibili.

Le coordinate astronomiche sono quelle che effettivamente sono misurate con il sistema del filo a piombo (o con il sestante); la verticale astronomica è la direzione del filo a piombo ed è perpendicolare al piano individuato dalla livella.
Dalla verticale si calcola l’altezza (h) della stella alla culminazione e, conoscendo la declinazione, è possibile ottenere la latitudine.

Latitudine e Longitudine¶
Il grande astronomo greco Ipparco (190-120 A.C.) per primo suggerì che per misurare la Terra si debba definire una rete geodetica regolare: inventò quindi un sistema di riferimento con meridiani e paralleli, da utilizzare per determinare una localizzazione: la latitudine e la longitudine. Suddivise l’angolo giro in 360 gradi (°), il grado in 60 minuti (') e il minuto in 60 secondi ("), usando il sistema babilonese (sessagesimale) che è un ottimo compromesso per conciliare la durata dell’anno solare (circa 365 giorni) con quello lunare (circa 30 giorni).
Propose di calcolare la latitudine in base al rapporto gnomone-ombra all’equinozio e la longitudine con l’osservazione del ritardo della fase totale dell’eclisse di sole come misura del tempo tra i due luoghi (la differenza tra tempo assoluto e tempo locale); cioè, se l’eclisse (evento unico, simultaneo in ogni punto) avviene ad ore locali differenti, queste differenze dipendono solo dalla longitudine. Il problema di non avere orologi accurati e sincronizzati non permetteva però di utilizzare questo metodo per la determinazione corretta della longitudine (problema risolto solo nel 1700).
 |
 |
Le coordinate geografiche possono essere definite come gli angoli che la verticale (filo a piombo) del luogo fa in riferimento ai piani fondamentali dell’equatore (latitudine) e del meridiano di Greenwich (longitudine).

Le coordinate astronomiche sono calcolate in genere in gradi sessagesimali: l’angolo di latitudine (distanza angolare dall’equatore) o di longitudine (distanza angolare dal primo meridiano) sono calcolari in gradi, minuti e secondi. I computer «preferiscono» invece le coordinate sessagesimali decimali, in cui i minuti e i secondi sono trasformati dalla scala in sessantesimi a quella decimale.
Una volta misurata la coordinata astronomica di un punto, esistono diverse modalità di esprimerla:
- i gradi sessagesimali (DMS), espressi in gradi, minuti e secondi, per esempio 45
°14'12";- i gradi sessagesimali decimali (DD) (o gradi decimali), in cui il grado rimane uguale, ma i minuti e i secondi sono trasformati in decimali in gradi; la coordinata sopra diventa 45
°,23666667;- le coordinate proiettate, che dipendono dalla proiezione e, in genere, esprimono la distanza (di solito in metri) dall’origine del sistema di proiezione (ed eventualmente dalla falsa origine). Dipendono dal datum geodetico e dal sistema di proiezione.
La trasformazione da gradi sessagesimali a gradi decimali è semplice in quanto basta utilizzare la seguente algoritmo:
- i gradi rimangono identici;
- i minuti vanno divisi per 60 e sommati ai gradi, i secondi vanno divisi per 3600 (cioè 60 x 60) e sommati al risultato precedente.
Nell’esempio (partendo da 45 ° 14 ' 12 "):
- 45
°rimangono 45°;- i 14 minuti vanno divisi per 60 (risultato 0,233333), i 12 secondi per 3600 (risultato 0,0033333):
- risultato finale: 45 + 0,233333 + 0,0033333 = 45
°,23666667
Calcolo inverso:
La trasformazione da gradi decimali a gradi sessagesimali è l’inverso di quanto fatto sopra:
- i gradi rimangono identici;
- la parte decimale va moltiplicata per 60, prendendo il valore intero come dato dei minuti; la parte decimale del calcolo precendete va moltiplicata per 60, in modo da trovare i secondi.
Nell’esempio (partendo da 45 °,23666667):
- 45
°rimangono 45°;- i 0,2366667 minuti vanno moltiplicati per 60 (risultato 14,2), con risultato 14
'; i 0,2 secondi moltiplicati per 60 (risultato 12",0):- risultato finale: 45
°14'12"
Non è possibile, invece, passare in maniera semplice da un sistema di coordinate proiettate ad un sistema di coordinate polari. Per questi casi si devono utilizzare sistemi GIS, che danno un risultato abbastanza corretto, almeno in prima approssimazione (utilizzano la trasformazione di Helmert o le formule di Molodensky -vedi più avanti).
Ellissoide e Geoide¶
La Terra non è perfettamente sferica, ma è leggermente schiacciata ai poli, formando un ellissoide: questo è stato determinato già nel 1600, mediante l’utilizzo del telescopio per le determinazioni degli angoli e di metodi di calcolo più precisi (tavole logaritmiche) per effettuare le triangolazioni.
Per determinare la forma dell’ellissoide si è infatti dovuto misurare direttamente la lunghezza di un grado lungo il meridiano in varie parti della Terra, a diversa latitudine, mediante metodi trigonometrici: infatti, se un grado (arco di meridiano) è uguale a tutte le latitudini, la Terra è sferica, mentre se è risulta diverso la Terra ha una forma di ellissoide.
La prima misura, effettuata in Francia da Picard e sviluppata poi da Cassini, ha portato alla determinazione della forma della terra come un uovo (ellissoide prolato), in quanto il segmento settentrionale era più corto di quello meridionale. Gli inglesi (Newton e Huygens), da un punto di vista teorico, insistevano correttamente invece che la Terra avesse una forma ad ellissoide schiacciato ai poli (ellissoide oblato).

Le misure effettuate poi dall’Accademia delle Scienze francesi, in Perù (zona equatoriale) e in Lapponia (zona artica) hanno permesso di verificare sperimentalmente che l’ellissoide schiacciato ai poli, come previsto da Newton e Huygens, era quello corretto.
Un grado di longitudine non è costante, ma decresce fino a zero, in corrispondenza dei poli. Usando lo sferoide di Clarke (1866), la distanza di un grado di longitudine all’equatore è di 111,321 Km mentre è di soli 55,802 km al 60° di latitudine (notare che si deve fare riferimento ad un ellissoide per queste misure).

Tabella delle misure di longitudine usando l’ellissoide WGS84: Misure da: Robinson et. al. (1995). Elements of Cartography (6th ed.). New York: John Wiley & Sons Inc.
| Latitudine | Kilometri | Longitudine | Kilometri |
|---|---|---|---|
| 0° | 110,57 | 0° | 111,32 |
| 10° | 110,61 | 10° | 109,64 |
| 20° | 110,70 | 20° | 104,65 |
| 30° | 110,85 | 30° | 96,49 |
| 40° | 111,04 | 40° | 85,39 |
| 0° | 111,23 | 50° | 71,70 |
| 60° | 111,41 | 60° | 55,80 |
| 70° | 111,56 | 70° | 38,19 |
| 80° | 111,66 | 80° | 19,39 |
| 90° | 111,69 | 90° | 0,00 |
La variazione della latitudine è dovuta solo allo schiacciamento della terra ai poli; quello di longitudine dovuta al convergere dei meridiani.
Il calcolo delle coordinate astronomiche, come abbiamo visto, è condizionato dalla direzione del filo a piombo (verticale), che a sua volta è sensibile al campo gravitazionale. Tuttavia, il campo gravitazionale terrestre non è uniforme, ma è influenzato dalla diversa densità nei diversi punti della terra. La superficie equipotenziale del campo gravitazionale passante per livello medio del mare è detta geoide e corrisponde ad un ipotetico mare, con densità e temperature costanti, non perturbato da maree o correnti, che ricopra tutta la Terra. La verticale (il filo a piombo) è sensibile a questo campo gravitazionale.
Di conseguenza, possiamo dire che la Terra ha la forma di un ellissoide deformato (il geoide), che tiene conto della diversa forza gravitazionale sulla superficie. Diversi ellissoidi (figure geometriche regolari) sono state calcolate come migliore approssimazione per zone limitate del mondo, mentre altri ellissoidi, utilizzati soprattutto nella determinazione della coordinata con i GPS, sono geocentrici e con deformazione mediata su tutto il mondo (per esempio, il WGS84)

Le varie misure effettuate dai geografi, nel tempo hanno portato alla costruzione di diversi ellissoidi di riferimento, con varie misure per il semi-asse maggiore e lo schiacciamento. Tali differenze, dovute al diverso valore del campo gravitazionale sulla superficie terrestre (differenza ellissoide-geoide, detta ondulazione), hanno portato alla determinazione di diversi ellissoidi “locali”, ottimizzati per la mappatura di zone limitate, dove la coincidenza tra il geoide e l’ellissoide è maggiore.
Bastano due informazioni per definire l’ellissoide (esempio, asse maggiore e asse minore). I geodeti utilizzano in genere il semi-asse maggiore (cioè il raggio all’equatore) e lo schiacciamento.
Tabella dei parametri degli ellissoidi più utilizzati e zona di riferimento:
| Nome | Raggio equatoriale | Schiacciamento | Zona di utilizzo |
|---|---|---|---|
| Airy (1830) | 6.377.563,396 | 1/299,3249646 | Gran Bretagna |
| Everest (1830) | 6.377.276,345 | 1/300,8017 | India, Birmania, Malesia |
| Bessel (1841) | 6.377.397,155 | 1/299,1528128 | Europa centrale, Cile, Indonesia, Giappone |
| Clarke (1866) | 6.378.206,4 | 1/294,9786982 | Nord America, Filippine |
| Clarke (1880) | 6.378.249,145 | 1/293,465 | Francia, Africa |
| Helmert (1907) | 6.378.200,0 | 1/298,3 | Egitto |
| Hayford - International (1924) | 6.378.388,0 | 1/297,0 | Europa |
| Krassowsky (1940) | 6.378.245,0 | 1/298,3 | Russia, Europa dell’est |
| Hough (1956) | 6.378.270,0 | 1/297,0 | |
| Fisher (1960) - Mercury | 6.378.166,0 | 1/298,3 | |
| WGS 66 (1966) | 6.378.145,0 | 1/298,25 | USA – tutto il mondo |
| GRS 67 (1967) | 6.378.160,0 | 1/298,247167427 | Australia |
| New International (1967) | 6.378.157,5 | 1/298,24961539 | |
| Fisher (1968) | 6.378.150,0 | 1/298,3 | |
| South American (1969) | 6.378.160,0 | 1/298,25 | |
| WGS 72 (1972) | 6.378.135,0 | 1/298,26 | USA – tutto il mondo |
| GRS 75 (1975) | 6.378.140,0 | 1/298,257 | Sud America |
| GRS 80 (1979-80) | 6.378.137,0 | 1/298,257222101 | Nord America |
| WGS 84 (1984) | 6.378.137,0 | 1/298,257223563 | USA – tutto il mondo |
Lo schiacciamento (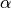 ) è definito da:
) è definito da:
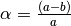
dove a = semi-asse maggiore e b = semi-asse minore, da cui
b = a (1 – 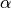 )
)
- La differenza tra ellissoide e geoide è dovuta a:
- scostamenti verticali (deflessione della verticale), dovuti alla differenza tra normale dell’ellissoide (linea perpendicolare alla superficie dell’ellissoide) e la verticale del geoide (ottenuta con il filo a piombo); ha due componenti (una in direzione nord-sud e l’altra in direzione est-ovest).
- scostamenti lineari tra le due superfici (ondulazione del geoide), che è uno scostamento altimetrico (esempio, la differenza tra altitudide del GPS e quella rilevata con metodi topografici).

Nell’immagine sotto viene evidenziata la differenza tra l’ellissoide WGS84 e il geoide (ondulazione) mediata sulla griglia di latitudine-longitudine di 10° (fonte: Defense Mapping Agency. 12 Jan 1987)

La differenza tra quota ortometrica e quota ellissoidica (ondulazione del geoide) può non essere elevata (in genere, tra i 2 e i 40 m), ma dà la differenza tra misure trovate con teodoliti (che si basano sul geoide e sull’altezza media del mare) e l’altezza data dai GPS (che viene calcolata sull’ellissoide WGS84).

Infine, l’ellissoide e il geoide non sono necessariamente centrati sul centro della Terra. La normale geodetica è perpendicolare alla superficie dell’ellissoide di riferimento utilizzato per misure geodetiche nel centro di emanazione mentre la verticale geocentrica è la direzione del raggio terrestre.
La differenza tra normalegeodetica e direzione del raggio terrestre (verticale geocentrica) dipende dallo schiacciamento polare della terra; l’angolo tra le due verticali prende il nome di “angolo della verticale” ed ha una sola componente (nord-sud) e il suo valore dipende dalla latitudine; è zero ai poli e sull’equatore e assume il valore massimo (11 ' 32,73 ") alla latitudine di 45°.

- Ne consegue che si possono determinare, per uno stesso punto sulla Terra, 3 diversi tipi di coordinate geografiche:
- coordinate astronomiche (la verticale è il filo da piombo, cioè si basa sul geoide);
- coordinate geodetiche (la verticale è la perpendicolare (normale) all’ellissoide, approssimazione locale del geoide);
- coordinate geocentriche (la verticale è la direzione del raggio terrestre; corrisponde alla verticale geodetica solo per gli ellissoidi centrati sulla terra).
Va comunque rimarcato che la verticale astronomica è quella operativa (viene effettivamente misurata in ogni punto), mentre le altre due sono concettuali, basandosi sull’approssimazione ideale della forma del globo (verticale geodetica) o sull’individuazione del centro della terra ideale (verticale geocentrica).
Il sistema GPS (e l’ellissoide / datum associato, cioè il WGS84) sono un esempio di sistema geocentrico, in quanto il baricentro delle orbite dei satelliti di triangolazione è coincidente con il centro terrestre.
Va ricordato che le differenze tra misura astronomica e coordinata fornita dal GPS o quella misurata con GoogleEarth (che si basano entrambi sull’ellissoide WGS84) può arrivare fino a 50 " in latitudine e 30 " in longitudine.
In conclusione, è importante dal punto di vista pratico sapere come si è ottenuta una coordinata di un punto (o di una linea / poligono), per esempio se deriva da un GPS od un calcolo sulla carta (con quale proiezione, ellissoide o datum geodetico?), perché in questo modo si può tenere conto del margine di errore nella trasformazione.
Datum geodetici¶
Il datum geodedico è in pratica una roto-traslazione dell’ellissoide di riferimento.
I diversi ellissoidi calcolati nelle varie aree della Terra sono stati utilizzati i calcoli di proiezione: per questa operazione si devono individuare un’origine e un sistema di riferimento delle coordinate. Il datum geodetico è individuato da questi parametri. Per esempio, l’Ellissoide di Clarke funziona meglio in Nord America, quello Internazionale di Hayford in Europa. I due datum nella figura sotto utilizzano due ellissoidi diversi, ma hanno anche diversa origine (il punto 0) e inclinazione del sistema di riferimento cartesiano.

La definizione classica di datum è quindi di un ellissoide orientato localmente: si sceglie un ellissoide che approssima in modo migliore l’area di studio, con parametri noti (semiasse maggiore e schiacciamento), che viene poi orientato in un dato punto (detto punto di emanazione).
- Nel punto di emanazione devono essere verificate queste condizioni:
- la normale ellissoidica coincide con la verticale;
- la direzione del meridiano ellissoidico coincide con quello astronomico;
- la quota ellissoidica coincide con quella ortometrica.
In pratica, questo vuol dire che in quel punto il geoide e l’ellissoide risultano tangenti.
- I datum orizzontali consistono nei seguenti parametri:
- longitudine e latitudine di un punto d’inizio (origine);
- azimuth di una linea (direzione) dell’origine rispetto ad alcune stazioni di triangolazione;
- ellissoide di riferimento (raggio e schiacciamento);
- separazione del geoide nell’origine.
Esempio di parametri iniziali del datum Roma 1940 (M.Mario)

Quindi, mentre nelle misurazioni geodetiche le posizioni relative tra punti sono correlabili, le distanze e gli azimuth derivate da calcoli con datum geodetici differenti saranno affette da errori proporzionali alle differenze tra i parametri iniziali sopra elencati: in pratica, misure effettuate mediante il GPS con il datum / ellissoide WGS84 non sono direttamente riportabili su una cartina geografica disegnata in base al datum geodetico Monte Mario 1940, ma occorre modificare i dati mediante delle trasformazioni (parametri di Helmert o formule di Molodensky) o, per essere più precisi, mediante dei grigliati, cioè matrici di trasformazione per la differenza locale tra i due sistemi.
I datum geodetici in genere sono utilizzati per la cartografia piana: sono detti datum orizzontali o planimetrici; in questi datum la quota è calcolata rispetto all’ellissoide (quota ellissoidica).
Nei datum verticali o altimetrici viene tenuto conto anche della quota ortometrica (o geoidica), cioè della differenza dovuta all’ondulazione del geoide; in questi datum quindi la quota è quella relativa al livello del mare. I datum verticali fanno riferimento ad un punto di origine, detto «caposaldo fondamentale» a cui viene assegnata la quota zero ed a una «rete di livellazione» composta da capisaldi che coprono l’area di rilevamento.
Proiezioni¶
Mentre un sistema di coordinate geografiche o polari (latitudine-longitudine) costituisce un sistema di riferimento utilizzabile da qualsiasi parte sulla Terra, i sistemi piani in genere sono utilizzabili solo su aree ristrette, a causa delle distorsioni introdotte nella proiezione. Tuttavia, se si devono fare misure o calcoli, le coordinate sferiche sono difficili da utilizzare, mentre la loro trasformazione in coordinate cartesiane permette di ottenere rappresentazioni della Terra più semplici da trattare. Queste trasformazioni equivalgono a rappresentare la superficie sferica (ellissoidica) del globo su una superficie piatta, con un processo detto di proiezione. In altre parole, la proiezione trasforma una superficie tridimensionale in una mappa bidimensionale; le formule di proiezione sono espressioni matematiche che convertono i dati da una localizzazione geografica (latitudine-longitudine) su una sfera o uno sferoide in coordinate cartesiane.
Dal punto di vista geometrico, questo significa prolungare (proiettare) un punto su una superficie piana (piano) o svolgibile in una superficie piana (cilindro, cono).

Analiticamente, una proiezione comporta la determinazione di due funzioni (f e g) che trasformino le coordinate polari (latitudine e longitudine), calcolate sull’ellissoide, in coordinate cartesiane (Est-Nord).

Per esempio, la funzione analitica che lega le coordinate in latitudine ( ) e la longitudine (
) e la longitudine ( ) con le coordinate x e y della longitudine per la proiezione ortografica con centro di origine (
) con le coordinate x e y della longitudine per la proiezione ortografica con centro di origine ( ,
,  ), semplificando il globo terrestre come una sfera con raggio R, è data dalle equazioni:
), semplificando il globo terrestre come una sfera con raggio R, è data dalle equazioni:
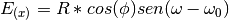
![E_{(y)} = R * [cos({\phi}_{0}) * sen ({\phi}) - sen({\phi}_{0}) * cos({\phi}) * cos ({\omega} - {\omega}_{0})]](_images/math/812c6dbb6d7ec4f8859da73522d387f534eefa79.png)
La proiezione produce inevitabilmente la distorsione di qualche caratteristica (forma, area, distanza, direzione). Ogni proiezione ha un’area di minor distorsione, che viene posizionata sull’area principale da cartografare, con opportuni spostamenti degli assi e punti di riferimento di proiezione. Quando si vogliono misurare delle caratteristiche, va quindi conosciuta la distorsione introdotta e di che entità è.
- Le mappe proiettate sono classificate in:
- conformi od isogone, quando conservano gli angoli (isogone o autogonali) e, come conseguenza, la forma (conformi o ortomorfe), almeno a livello locale. Le linee del reticolo geografico sono perpendicolari. Le aree possono invece essere molto distorte. Nessuna mappa riesce a mantenere le forme per regioni molto grandi;
- equivalenti (o equiareali o autaliche), quando mantengono le aree alla stessa scala. Per ottenere questa proprietà vengono però distorte le altre (forma, angoli, distanze). I meridiani e i paralleli possono incrociarsi non ad angolo retto. Anche se la condizione di equivalenza non può esistere contemporaneamente a quella di conformità, per piccole regioni sono quasi indistinguibili;
- equidistanti (o lineari), quando mantengono le distanze lungo una particolare direzione; tali lunghezze sono dette omologhe. Nessuna proiezione conserva la scala su tutta la mappa, ma spesso viene mantenuta lungo una o più linee (equatore o meridiani, grandi circoli o altre linee). Alcune mappe mantengono la scala solo tra uno o due punti verso tutti gli altri della mappa (two_point_equidistant);
- a direzione vera o azimutali, se rappresentano certe direzioni in maniera accurata; la linea più corta tra due punti è il grande circolo che passa tra i due; queste proiezioni rendono diritti alcuni dei grandi circoli, indicando la direzione (azimuth) di tutti i punti sulla mappa correttamente rispetto al centro.
- Si dicono poi afilattiche le proiezioni che realizzano un compromesso accettabile, minimizzando i vari tipi di deformazione; per contro, in queste sono presenti tutte le possibili deformazioni.
Un modo semplice ed intuitivo per rappresentare le deformazioni su una mappa è quello di usare la indicatrice di Tissot: è l’ellisse disegnato in carta che corrisponde al cerchio tracciato sulla superficie dell’ellissoide. In questo modo è possibile verificare graficamente, in ogni punto, il grado di deformazione nelle varie direzioni. Nelle proiezioni conformi è un cerchio (forma mantenuta), la cui area indica le dilatazione o contrazioni prodotte dalla proiezione.

- Le proeiezioni scelte per le mappe topografiche devono mantenere valide le seguenti assunzioni (assunti di scala planimetrica):
- la mappa ha una scala uniforme che può essere usata per misurare distanze;
- la forma degli oggetti rappresentati è una ragionevole approssimazione di quella reale;
- le direzioni dei punti cardinali sono ad angolo retto tra loro.
Questi assunti sono gli stessi di un sistema di coordinate cartesiano, che permette di misurare distanze utilizzando la geometria piana.
Classificazione delle proiezioni¶
I tipi più semplici di proiezioni sono fatti su forme geometriche che possono essere appiattite senza stirare la loro superficie (cioè possono diventare piatte semplicemente aprendole, senza deformazioni, come cilindri o coni o superfici già piane). Tutte le superfici utilizzate nelle proiezioni sono sezioni coniche.
- Il primo passo per proiettare una superficie su un’altra è quello di creare uno o più punti di contatto (detti punti di tangenza):
- le proiezioni piane possono essere tangenti ad una sfera solo in un punto;
- le proiezioni coniche e cilindri sono in contatto con la sfera lungo una linea.
Se invece la superficie proiettiva “entra” nel globo, si hanno proiezioni secanti. In ogni caso, tangenti o secanti, il punto o la linea di contatto sono importanti, in quando definiscono i punti o le linee a distorsione nulla. Questa linea è definita standard line.
Le proiezioni possono essere classificate sulle modalità di costruzione:
superficie geometrica di proiezione (piane, cilindriche, coniche);
orientamento della superficie di proiezione rispetto alla superficie terrestre (dirette, trasverse, oblique);
posizione della superficie di proiezione rispetto alla superficie terrestre (tangente, secanti);
posizione del punto di vista che origina la proiezione, rispetto al globo terrestre (centrografiche, stereografiche, scenografiche, ortografiche);
modo geometrico o matematico per la costruzione della proiezione (vere, modificate, convenzionali). Vere quando il reticolato è costruito solo con uso di principi geometrici; modificate quando le deformazioni ottenute dal metodo precedente vengono ridotte con formule matematiche; nelle convenzionali od analitiche, la costruzione della mappa avviene non con formule proiettive, ma mediante relazioni matematiche ad hoc.
Coniche¶
La proiezione conica più semplice è quella tangente al globo lungo una linea di latitudine. Questa linea è allora detta parallelo standard.
- Nelle proiezioni coniche:
- I meridiani sono diritti e convergenti, incontrandosi all’apice.
- I paralleli della latitudine sono archi concentrici.
Il meridiano opposto alla linea di taglio diventa il meridiano centrale.
In generale la distorsione aumenta a nord e a sud del parallelo di tangenza; di solito queste aree vengono tagliate (per esempio, le zone polari quando il parallelo standard è nelle zone a latitudine media). Le proiezioni secanti sono definite da due paralleli standard (il cono interseca il globo lungo due linee). Anche in questo caso, allontanandosi dalle linee di secanza, le distorsioni aumentano.
Le più usate sono le proiezioni coniche polari, con l’asse del cono sull’asse terrestre; descrivono meglio le aree a latitudine media.
- Proiezione conica semplice (equidistant conic projection): Ottenuta con un cono tangente lungo un parallelo. È equidistante lungo i meridiani, cioè la distanza tra paralleli è sempre uguale; Forme ed aree sono ragionevolmente conservate, almeno non troppo lontano dal parallelo di tangenza.
Nell’esempio (codifica proj.4): +proj=eqdc +lat_1=30 +lat_2=50 +lat_0=0 +lon_0=0 +x_0=0 +y_0=0 +datum=WGS84 +units=m

- Proiezione conica equivalente di Albers: Ottenuta dallo sviluppo di un cono secante lungo due paralleli. Rappresenta le aree in modo corretto e ha modeste deformazioni tra due paralleli di secanza. La distanza tra paralleli diminuisce, allontanandosi dalle linee di decanza.
Nell’esempio (codifica proj.4): +proj=aea +lat_1=30 +lat_2=50 +lat_0=0 +lon_0=0 +x_0=0 +y_0=0 +datum=WGS84 +units=m

- Proiezione conica conforme di Lambert: Ottenuta dallo sviluppo di un cono secante lungo due paralleli. Paralleli e meridiani si intersecano ad angolo retto ed in ogni punto la scala è uguale in ogni direzione. La distanza tra paralleli aumenta sempre più verso il bordo del cono, ma le forme sono mantenute.
Nell’esempio (codifica proj.4): +proj=lcc +lat_1=30 +lat_2=50 +lat_0=0 +lon_0=0 +x_0=0 +y_0=0 +datum=WGS84 +units=m

Cilindriche¶
Le proiezioni cilindriche, come le coniche, possono avere una linea di tangenza o due linee di secanza lungo il globo. Si ottengono dallo sviluppo in piano di una superficie di un cilindro. Sono molto utilizzate, sia con cilindro con asse coincidente con l’asse terrestre (cilindriche dirette, tangenti all’equatore) che orientato perpendicolarmente (cilindriche trasverse, tangenti ad un meridiano).
- Nelle proiezioni cilindriche dirette:
- i meridiani e i paralleli si intersecano ad angolo retto e il reticolato è rettangolare. Lungo la linea equatoriale sono rispettati i rapporti di equidistanza, mentre i poli sono rappresentati da una linea.
- Nelle proiezioni cilindriche trasverse:
- i meridiani e i paralleli sono archi (ad eccezione di quelli centrali, che sono linee dritte) che si intersecano ad angolo retto, ma il reticolato non è rettangolare.
- Le variazioni tra le varie proiezioni riguardano la diversa spaziatura dei paralleli:
- cilindriche vere, dove i paralleli tendono ad infittirsi verso i poli, mentre i meridiani sono spaziati in maniera costante; ne segue una progressiva esagerazione delle distanze e delle forme in senso est-ovest;
- cilindriche centrali, dove i paralleli si distanziano maggiormente verso i poli, con esagerazione progressiva delle distanze e delle forme in senso nord-sud;
- proiezione di Mercatore (modificata), dove la distanza tra paralleli è calcolata matematicamente in modo da produrre una distorsione nord-sud che compensa quella est-ovest.
- Proiezione cilindrica semplice; Equirettengolare o Plate Carrée. La cilindrica semplice è equidistante (conserva la scala) lungo tutti i meridiani, spaziati in modo uguale ai paralleli (reticolo a maglie quadrate). Regione polare presenta una forte distorsione in senso est-ovest
Nell’esempio (codifica proj.4): +proj=eqc +lat_ts=0 +lat_0=0 +lon_0=0 +x_0=0 +y_0=0 +datum=WGS84 +units=m

- Proiezione di Mercatore. I meridiani e i paralleli di incrociano ad angolo retto; all’equatore le distanze sono proporzionali a quelle reali. Le distanze tra paralleli aumentano verso i poli, compensando la deformazione est-ovest dei meridiani: il fattore di scala risulta quindi uguale in tutte le direzioni (proiezione isogona e conforme). Le aree verso i poli sono molto esagerate. Le linee di identica direzione (azimuth) incontrano i meridiani con angolo costante (lossodromia).
Nell’esempio (codifica proj.4): +proj=merc +lon_0=0 +k=1 +x_0=0 +y_0=0 +a=6378137 +rf=298.257223563 +towgs84=0.000,0.000,0.000 +to_meter=1

- Proiezione trasversa di Mercatore: Ottenuta da un cilindro con asse perpendicolare all’asse terrestre. Lungo il meridiano di tangenza le distanze sono proporzionali a quelle reali. Lungo i paralleli la distorsione aumenta allontanandosi dal meridiano centrale. È la base per la definizione del reticolo UTM, in cui le varie zone sono separate ogni 6° di longitudine.
Nell’esempio (codifica proj.4): +proj=tmerc +lat_0=0 +lon_0=0 +k=1 +x_0=0 +y_0=0 +datum=WGS84 +units=m

Piane o Azimutali¶
Proiettano il globo su una superficie piana, in genere tangente in un punto (ma può essere secante). Sono dette anche azimutali, in quanto vengono mantenuti gli angoli di direzione (azimuth) rispetto al punto centrale della proiezione. Di conseguenza, tutti i circoli massimi passanti per il centro della proiezione sono rette. Il punto di contatto è detto fuoco, identificato da una longitudine e latitudine centrali; il fuoco definisce anche l’aspetto, che può essere polare (il fuoco è un polo), equatoriale (un punto sull’equatore) od obliquo (qualsiasi coordinata tra i poli e l’equatore).
- Le proiezioni piane sono in genere dette anche prospettiche, in quanto sono effettive proiezioni geometriche da un punto di vista, e si classificano in base a:
- posizione del punto di vista (gnomonica, dal centro della Terra), stereografica (dagli antipodi del centro di tangenza) o ortografica (dall’infinito);
- dall’orientamento (o aspetto): polare, equatoriale, obliquo;
- Sono usate spesso per la rappresentazione delle aree polari:
- i paralleli sono rappresentati come cerchi concentrici,
- i meridiani come rette che si intersecano ai poli con il loro vero angolo di direzione.
Nelle equatoriali il reticolo geografico si incontra al fuoco con un angolo di 90°. Le direzione dal fuoco sono accurate; la distanza minore dal fuoco ad un altro punto è la linea retta. Le distorsioni angolari e areali hanno andamenti varianti con la distanza dal fuoco.
- Gnomonica: È caratterizzata da forti aumenti delle lunghezze e dimensioni delle aree dal fuoco. Gli archi di circonferenza (linee più brevi tra due punti o linee ortodromiche) sono rappresentati come rette; Utilizzata appunto per questo per la navigazione aerea.
Nell’esempio (codifica proj.4): +proj=gnom +lat_0=90 +lon_0=0 +x_0=0 +y_0=0 +datum=WGS84 +units=m

- Ortografica: Diversamente dalla gnomonica, le lunghezze e le aree diminuiscono allontanandosi dal fuoco. Le zone lontane dal fuoco sono fortemente compresse. Queste forte deformazioni nelle zone periferiche la rendono poco utile, se non per rappresentazioni della Terra.
Nell’esempio (codifica proj.4): +proj=ortho +lat_0=0 +lon_0=0 +x_0=0 +y_0=0 +datum=WGS84 +units=m

- Stereografica: Caratterizzata da distanze costanti allontanandosi dal fuoco. I meridiani e i paralleli si incrociano ad angolo retto: di conseguenza è conforme. La scala aumenta allontanandosi dal centro, anche molto nelle zone periferiche. La stereografica con aspetto polare è la base per la definizione del reticolo UPS (Universal Polar Stereographic), l’equivalente dell’UTM per le zone polari.
Nell’esempio (codifica proj.4): +proj=stere +lat_0=0 +lon_0=0 +k=1 +x_0=0 +y_0=0 +datum=WGS84 +units=m

Scala e Risoluzione¶
Scala di una mappa
Per rappresentare una porzione della superficie della Terra su una mappa, l’area deve essere ridotta: la scala della mappa indica il rapporto di questa riduzione. Le mappe sono cioè rappresentazioni semplificate e ridotte della realtà geografica.
La scala di una mappa permette di conoscere il grado di approssimazione alla realtà. Le scale sono rappresentate in 4 modi:
- frazione rappresentativa (representative fraction): è mostrata come 1 (mappa) : numero (realtà) (esempio, 1 : 10.000). Significa che 1 unità di mappa corrisponde a x unità sulla superficie terrestre. Per esempio, 1 mm in scala 1:10000 corrisponde a 10000 mm, cioè a 10 metri. Si possono utilizzare le unità che si vogliono: quindi 1 cm, nella stessa scala, corrisponde a 10000 cm, cioè a 100 metri;
- affermazione verbale (verbal statement): corrisponde alla precedente, ma è esplicitata in maniera verbale. Per esempio, si può dire “1 cm di mappa è uguale a 100 metri”;
- barra o grafico di scala (bar o graph scale): è un simbolo (in genere una linea o un rettangolo) con segnali in corrispondenza dei valori di distanza reale.
- area in scala (area scale): è il rapporto tra l’area sulla mappa e l’area rappresentata in realtà (ovviamente usata solo nelle proiezioni equivalento, o equal-area). In questo caso, se in una scala di 1:20.000 (in frazione rappresentativa) 1 mm corrisponde a 20.000 mm, 1 mm2 corrisponderà a 20.000 x 20.000 mm2, cioè a 400 m2
La frazione rappresentativa è uno dei modi più usati per esprimere una scala e indica di quanto un’area terrestre è stata ridotta. Per esempio, una mappa delle stesse dimensioni gli oggetti rappresentati sono molto più piccoli in una mappa a piccola scala (esempio 1:1.000.000) rispetto ad una a larga scala (1:2.000)
Su molte mappe sono riportate le griglie cartografiche, come l’UTM. Questo permette di verificare la scala della mappa.
Per calcolare la scala di una mappa, conosciuta la distanza reale, basta misurare il valore corrispondente in mappa ed usare la formula:
1 / RFD = (MD * CON) / GD
dove, FRD = denominatore della frazione rappresentativa MD (map distance) = distanza sulla mappa GD (ground distance) = distanza al suolo CON = fattore di conversione tra unità con cui si misura la mappa e quelle al suolo
Per esempio, se 4 centimetri (MD) corrispondono a 10 km, cioè 10000 m (GD), CON è 1/100000 (rapporto tra cm e kilometri) e quindi: (4 * 1/100000) / 10 = 0,000004, il cui inverso 250000.
La scala è quindi di 1 / 250000.

Risoluzione di una mappa
Anche se un GIS non ha apparentemente scala, nel senso che il geodataset di un GIS non aumenta o si riduce in funzione della scala, tuttavia è caratterizzato dalla scala di acquisizione (o di input), cioè dal grado della sua generalizzazione: quindi, anche se il geodataset è senza scala, quando si visualizza o si stampa una mappa non si può stare molto lontani dalla scala di acquisizione.
Nell’esempio sotto è evidente l’insufficienza della mappa a scala più piccola, lontana dalla scala di acquisizione.
| Scala acquisizione | Ingrandimento |
|---|---|
 |
 |
La risoluzione di una mappa si riferisce a quanto accuratamente le localizzazioni e le forme degli oggetti possono essere rappresentate ad una data scala. Se nei GIS le mappe possono essere visualizzate o stampate a vari ingrandimenti, è importante tenere presente che l’accuratezza della digitalizzazione o del dato acquisito non permette di andare oltre un certo limite.
Gli oggetti disegnati su una mappa a larga scala sono molto più rassomiglianti alla realtà rispetto ad una su piccola scala: diminuendo la scala, infatti, gli oggetti hanno forme e aspetti più semplificati (i fiumi diventano semplicemente linee e i paesi sono rappresentati da punti) o possono anche non essere rappresentati del tutto (esempio, un piccolo stagno su una scala 1:100.000).
Per valutare la scala in un GIS, si devono tener presenti i dati di partenza: se una mappa è stata digitalizzata o acquisita come raster da una mappa 1:100.000, ci saranno parecchi problemi ad utilizzarla con altre mappe ottenute in scala di partenza 1:10.000, in quanto il grado di generalizzazione degli oggetti digitalizzati è direttamente proporzionale alla scala. Idealmente, si dovrebbe già sapere quale deve essere la scala delle mappe finali di output, in modo da tenerne conto nell’acquisizione dei dati (che devono corrispondere o essere leggermente a scala maggiore).
La misura e le dimensioni minime rappresentabili sono dette unità minime di mappa (minimum mapping units). In genere le strutture più piccole di circa 0,2 cm (in unità di mappa) non sono rappresentabili:
| Scala | 0,2 cm (lineare) | Superfici |
|---|---|---|
| 1 : 10.000 | 0,02 Km (20 m) | 0,04 ha (400 mq) |
| 1 : 50.000 | 0,1 Km (100 m) | 1 ha |
| 1 : 100.000 | 0,2 Km (200 m) | 4 ha |
| 1 : 250.000 | 0,5 Km (500 m) | 25 ha |
| 1 : 1.000.000 | 2 Km | 400 ha (4 Kmq) |
Impostazione CSR¶
L’impostazione del sistema di riferimento delle coordinate (CRS Coordinate Reference System) viene in genere effettuato alla creazione del progetto (.qgs). All’apertura di QGIS, il sistema di default impostato è il WGS84, con unità in gradi di longitudine e latitudine.
Il sistema di riferimento delle coordinate è indicato a destra, nella barra di stato, mediante l’utilizzo del codice EPSG:

L’EPSG (European Petroleum Search Group) mette a disposizione un database con le definizione dei sistemi di riferimento delle coordinate (CRS) a livello globale, regionale, nazionale e locale, in formato Well-Known-Text, WKT (ISO 19162). Il dataset può essere scaricato in vari formati (MS Access, MySQL, Oracle, PostgreSQL) e viene aggiornato in genere due volte all’anno. QGIS utilizza questo database, contenente più di 2700 CRS, per l’impostazione del sistema di riferimento: viene caricato durante l’installazione, in formato SQLite.
Qui sotto la selezione delle informazioni della tabella dei CRS del database:

Nel database, oltre alle definizioni del CRS in WKT (leggibile anche dalle librerie proj.4 e GDAL), viene definito un numero identificativo univoco, che può essere utilizzato per impostare il CRS: per esempio, il WGS 84, unità in latitudine/longitudine ha codice 4326.
Conviene sempre decidere quale sistema di riferimento si intende utilizzare e trasformare in seguito tutti i layer con cui si lavora nel sistema di riferimento scelto. Ogni trasformazione del sistema di riferimento (riproiezione) introduce sempre degli errori (vedi più avanti).
L’impostazione del sistema di riferimento del progetto avviene utilizzando il comando in fondo a destra, nella barra di stato  , oppure in [MT -> Progetto -> Proprietà progetto -> SR]
, oppure in [MT -> Progetto -> Proprietà progetto -> SR]
In entrambi i casi, viene aperta l’interfaccia di impostazione del sistema di riferimento delle coordinate. Abilitando la riproiezione al volo si attivano le opzione di impostazione del sistema, da cui si può scegliere la proiezione o il datum del progetto.

La ricerca attraverso il database EPSG è facilitata dall’utilizzo dei filtri.
Si può cercare il sistema di riferimento mediante il nome (per esempio, Mario per cercare il datum Monte Mario, 1940):

Oppure mediante il codice EPSG (o una parte):

Selezionando il sistema di riferimento, nella casella in fondo compare la sua definizione con il codice proj.4:

- I CRS usati recentemente sono mostrati nella finestra in alto, in modo da facilitare la selezione di quelli più utilizzati. Nella finestra centrale sono riportati tutti i CRS caricati nel database, raggruppati in tre tipologie:
- Sistemi di coordinate geografiche: CRS che utilizzano le coordinate geografiche;
- Sistemi di coordinate proiettate: CRS che utilizzano le coordinate cartesiane, in base ad una proiezione;
- Sistemi di coordinate definiti dall’utente.

Il CRS selezionato è mostrato con il nome (in alto) e con la definizione proj.4:

Quando viene definito il CRS del progetto, QGIS automaticamente cambia le impostazioni delle unità nelle Proprietà del Progetto.
| CRS con coordinate geografiche | CRS con coordinate proiettate |
|---|---|
 |
 |
- In QGIS valgono le seguenti definizioni:
- proiezione globale di default: la proiezione globale viene impostata quando si crea un progetto. Il CRS di default è EPSG:4326 - WGS 84 (proj=longlat +ellps=WGS84 +datum=WGS84 +no_defs);
- proiezione di progetto: CRS definito a livello di progetto;
- proiezione del layer: CRS del layer;
La proiezione globale di default può essere cambiata in [MT -> Impostazioni -> Opzioni -> SR] e vale anche per le successive sessioni di QGIS.
- Nella stessa finestra è possibile definire anche il CRS di default per i layer e il comportamento nel caso il CRS non sia riconosciuto:
- chiedi il CRS;
- usa il CRS del progetto;
- usa il CRS di default, impostabile con una casella a cascata.

Il sistema di riferimento del progetto può essere diverso da quello del layer (vettoriale, raster) importato nello stesso progetto. La funzione OTF, cioè (On-The-Fly, «al volo») mette in registro un layer (se riconosce il suo sistema di riferimento delle coordinate) sul sistema di riferimento del progetto.
- La funzione OTF, una volta abilitata:
- mette in registro automaticamente il layer se viene riconosciuto da QGIS (ad esempio mediante il file .qpj);
- mette in registro il layer quando viene manualmente assegnato il sistema di riferimento corretto.
Il supporto OTF è valido sia per layer vettoriali che raster, ma non è attivato di default; l’impostazione avviene nella finestra di impostazione dei CRS.
| Progetto senza OTF | Progetto con OTF attivato |
|---|---|
 |
 |
Quando non è attivato, il layer è caricato senza alcuna trasformazione delle coordinate.
- Ci sono 3 modi per attivare la trasformazione OTF:
- da [MT -> Progetto -> Proprietà del progetto -> SR]
- dall’icona in fondo a destra, nella barra di stato
- da [MT -> Impostazioni -> Opzioni -> SR], selezionando in «SR predefinito nei nuovi progetti» l’opzione «Automatically enable OTF if layers have different CRS» (attiva automaticamente proiezione al volo se i layer hanno CRS differente) o «Effettua sempre la riproiezione al volo»
Nei primi due casi, va attivata la casella «Enable on the fly CRS transformation (OTF) » (Attiva proiezione al volo)

Nell’esempio sotto viene caricato un layer di SpatiaLite (in cui il sistema di riferimento viene impostato alla creazione), che viene riconosciuto e messo a registro senza problemi: nella pagina delle proprietà si può controllare il CRS:

Non tutti i layer hanno un CRS che QGIS riesce ad interpretare; per esempio, gli shapefile devono avere un file di estensione .prj che non è sempre riconosciuto da QGIS (che utilizza il formato .qpj, più completo). Entrambi i file sono in formato testo (WKT, vedi più avanti); nella tabella sotto sono indicate le differenze tra i due formati per uno shapefile proiettato nel sistema UTM - zona 32 Nord e datum ETRS89 (EPSG: 25832):
| file prj | file qpj |
|---|---|
 |
 |
Se il CRS del layer non è riconosciuto, può essere impostato manualmente, sia per i vettori che per i raster, con tasto-dx-mouse sul layer nel pannello, che apre la finestra di impostazione del CRS.

Cliccando su «Imposta il SR del progetto dal layer» cambia il sistema di riferimento del progetto, impostandolo su quello del layer.
Il database dei CRS (EPSG) non va modificato; se serve un CRS personalizzato, questo deve essere aggiunto al database, senza modificare le definizioni dei sistemi di riferimento già caricati.
- La definizione di un nuovo CRS richiede la conoscenza della libreria proj.4, in modo da inserire correttamente i parametri necessari. Per inserire un nuovo CRS si devono inserire due informazioni:
- un nome descrittivo;
- i parametri cartografici in formato proj.4 (+proj= seguito dalle definizioni).
Il sito Spatial Reference può essere utilizzato per verificare le definizioni dei diversi sistemi di coordinate:
Si possono con un filtro cercare i CRS già definiti (in genere già inseriti in QGIS). Una volta trovato il CRS di interesse, si possono verificare le definizioni dei parametri, in vari formati:

Per impostare un CRS personalizzato si utilizza [MT -> Impostazioni -> SR Personalizzato]

I CRS personalizzati sono salvati nel database utente di QGIS (.qgis/qgis.db) in formato SQLite.

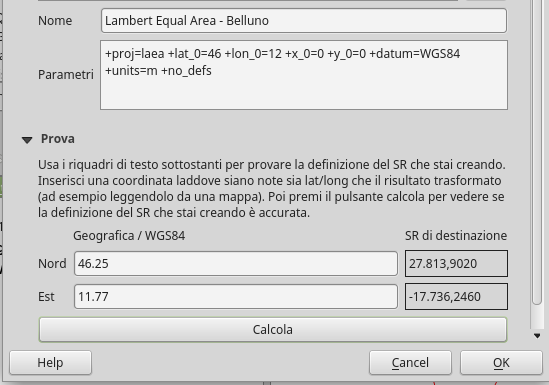
Per inserire le definizione del CRS personalizzato si deve cliccare sul tasto +

In fondo alla finestra dei SR personalizzati, è possibile inserire le coordinate di un punto in latitudine/ longitudine e datum WGS84 e calcolare i valori risultanti in base al nuovo CRS. Si possono verificare quindi se si ottengono i valori attesi:
Conversione tra ellissoidi e datum¶
I diversi sistemi di coordinate e/o di proiezione possono essere convertiti tra loro, se si conoscono i parametri del sistema.
- La conversione tra coordinate dipende dal tipo di coordinate di partenza:
- coordinate geografiche (latitudine e longitudine), misurate su uno specifico datum a partire dall’equatore e da Greenwich e con altitudine h, rispetto da un sistema di riferimento altimetrico (esempio mareografo di Genova);
- coordinate cartesiane geocentriche (X, Y, Z), calcolate rispetto ad uno specifico datum;
- coordinate piane (Est e Nord), derivanti da una mappa proiettata.
La trasformazione di coordinate piane (Est-Nord) in coordinate geografiche (latitudine-longitudine) riferite ad uno stesso datum è una semplice operazione matematica (praticamente l’inverso della proiezione).
La trasformazione di coordinate (piane o geografiche) tra datum diversi è invece complessa (comprende traslazioni, rotazioni e scalature) e introduce necessariamente degli errori di approssimazione.
- In pratica, l’operazione di conversione tra coordinate segue il seguente schema:
- effettuazione della proiezione inversa, da coordinate proiettate (Est-Nord) a coordinate geografiche (latitudine-longitudine) e trasformazione in geocentriche (X,Y,Z);
- operazione di rotazioni, traslazioni e scalature tra coordinate geocentriche di datum / ellissoidi diversi (da X,Y,Z a X”, Y”, Z”);
- proiezione delle coordinate geocentriche (X”, Y”, Z”) a coordinate piane (Est” – Nord”), mediante proiezione.

I modi di trasformazione tra tipi di coordinate seguono procedimenti diversi, a seconda delle coordinate di partenza e di arrivo, come evidenziato sotto:

- Le coordinate proiettate piane (Est-Ovest) possono essere convertite direttamente tra loro mediante formule approssimate a validità locale o mediante costanti di trasformazione appositamente tabulate (trasformazioni polinomiali a 3 parametri).
- Le coordinate geografiche (latitudine-longitudine) possono essere convertite tra loro mediante le formule di Molodenskii e sulla base di parametri appositamente calcolati (per esempio, da IGM o da NIMA) - trasformazioni a 5 parametri.
- Le coordinate geocentriche (X, Y, Z) possono essere convertite tra loro mediante formule approssimate a validità locale, ottenute mediante regressioni tra coordinate dei due sistemi (trasformazioni di Helmert a 7 parametri).
In QGIS, la trasformazione OTF utilizza il WGS84 (default CRS) come base: se il CRS del layer caricato non ha algoritmi di trasformazione verso il WGS84 non può essere messo a registro, a meno di fornire i parametri della trasformazione.
I parametri di trasformazione sono impostabili in [MT -> Impostazioni -> Opzioni -> SR]

- Le opzioni sono:
- casella per chiedere la definizione della modalità di trasformazione, se non è definito un default;
- finestra per impostare i parametri personalizzati di trasformazione.
Proj.4 supporta trasformazioni tra datum a 3 o 7 parametri per la maggior parte dei sistemi di coordinate supportati da EPSG http://www.epsg.org/ .
Permette anche la trasformazione di datum specifici, attraverso i grigliati. Incorpora anche quelli che sono free (purtroppo, non quelli dell’IGM che sono free solo per le pubbliche amministrazioni).
La proiezione OTF non trasforma il CRS del layer; per la trasformazione definitiva in un altro CRS si deve utilizzare il Salva con nome, definendo il nuovo CRS
| Trasformazione vettore | Trasformazione raster |
|---|---|
 |
 |
Plugin Catture Coordinate¶
Il Plugin Cattura coordinate ha un utilizzo intuitivo e permette di visualizzare le coordinate «catturate» con il mouse sull’area di mappa, per due CRS selezionabili. Va attivato nel plugin Manager [MT -> Plugins -> Gestisci ed installa Plugins].

Una volta attivato, il plugin compare nel pannello dei layer. Per selezionare un altro sistema di riferimento, rispetto a quello impostato per l’area di mappa di QGIS, basta cliccare su bottone  .
.

Premendo sul bottone  è possibile, cliccando una qualsiasi parte dell’area di mappa di QGIS, rendere visibili nelle finestre del pannello le coordinate dei due CRS selezionati.
è possibile, cliccando una qualsiasi parte dell’area di mappa di QGIS, rendere visibili nelle finestre del pannello le coordinate dei due CRS selezionati.

Per mostrare il cambiamento delle coordinate allo spostarsi del puntatore del mouse, cliccare su  .
.
Infine, con il bottone  , è possibile memorizzare i dati, per poterli poi copiare in un nuovo software (foglio di calcolo, word processor, ecc.)
, è possibile memorizzare i dati, per poterli poi copiare in un nuovo software (foglio di calcolo, word processor, ecc.)

Principali sistemi di riferimento¶
I sistemi di riferimento delle coordinate (Coordinate Referencing Systems o CRS) servono per definire univocamente le localizzazioni e le forme degli oggetti sulla superficie della Terra. Alcuni sistemi sono ben definiti e usati comunemente, per cui è importante conoscere le loro caratteristiche. In genere il sistema di riferimento è calcolato in modo di avere sempre valori positivi (aggiungendo una falsa origine sull’asse delle x o delle y). Per esempio, il sistema Gauss-Boaga italiano aggiunge 1.500.000 m alla coordinata x (easting) per il fuso ovest e 2.520.000 m per il fuso est.
Tra questi sistemi di riferimento sono importanti le proiezioni geodetiche, cioè quelle utilizzate a grande scala per le misure locali e che fanno riferimento ad ellissoidi e datum locali. In genere utilizzano proiezioni cilindriche trasverse.
Pseudo Mercatore¶
Detto anche WGS 84 / Popular Visualisation Pseudo-Mercator o Web Mercator.
- (EPSG: 3857): +proj=merc +a=6378137 +b=6378137 +lat_ts=0.0 +lon_0=0.0 +x_0=0.0 +y_0=0 +k=1.0 +units=m +nadgrids=@null +wktext +no_defs
Non è un sistema geodetico, in quanto la Terra è modellizzata come una sfera perfetta (infatti, i due semi-asso - parametro +a e il parametro +b - si equivalgono e sono messi pari a 6378137). Viene utilizzato per la cartografica nel web (Google Earth), in quanto i calcoli sono più veloci rispetto all’uso dell’ellissoide. Di conseguenza, le misure fatte con questa proiezione sono approssimative (eccetto all’equatore) e l’aspetto di un quadrato disegnato sulla superficie varia con la latitudine.
Può essere utilizzata tra la latitudine 85.06°S e 85.06°N.

Rispetto alla proiezione di Mercatore, con ellissoide WGS84, possono esserci differenze fino allo 0,7% in scala, pari a circa oltre 45 km. Sotto le due proiezioni sono sovrapposte per mostrare la differenza:

Sistema e Proiezione UTM¶
Il sistema UTM (Universal Transverse Mercator) è valido per tutta la superficie terrestre, anche se nelle zone polari, oltre l’80° parallelo, viene sostituito dall’UPS (Universal Polar Stereographic).
Usa la proiezione di Gauss (cilindrica trasversa).
Il sistema UTM ha diversi codici EPSG, in base al datum di riferimento e alla zona:
- (EPSG: 32632): +proj=utm +zone=32 +datum=WGS84 +units=m +no_defs - WGS 84 / UTM zone 32N
- (EPSG: 23033): +proj=utm +zone=33 +ellps=intl +towgs84=-87,-98,-121,0,0,0,0 +units=m +no_defs - ED50 / UTM zone 33N
Il mondo è stato suddiviso in 60 fusi di 6° di ampiezza, ciascuno attorno ad un meridiano di riferimento (meridiano centrale). I fusi sono numerati progressivamente ad ovest ad est, a partire dall’antimeridiano di Greenwich: quindi il fuso 1 ha come meridiano centrale il 177° ovest (180° - 3°), il fuso 32 ha come meridiano centrale il 9° est. L’Italia è compresa nei fusi 32, 33 e 34.
La coordinata, nel sistema UTM viene indicata nel seguente modo:
| Zona | Emisfero | Falso est (m) | Falso nord (m) |
| 32 | Nord | 527061 | 5063654 |
Questo punto è localizzato nella zona 32Nord, con coordinata E370823 e N4315291
Il pianeta è stato poi suddiviso, dall’80° parallelo nord all’80° sud in 20 fasce di 8° di latitudine, indicate con le lettere dell’alfabeto inglese da C a X (fascia C da 80°S a 72°S, fascia T da 40° N a 48° N).

L’intersezione tra fusi e fasce determina le zone, individuate da numero del fuso + lettera della fascia: esempio, zona 32T. L’Italia è compresa nelle fasce T ed S.

Il sistema UTM è utilizzato con vari datum, in tutto il mondo ed è stato adottato del sistema militare NATO MGRS (Military Grid Reference System) che utilizza una diversa codifica, suddividendo in fusi e fasce (per esempio, zona 32T), all’interno della quale esiste una suddivisione in quadrati di 100 km, codificati con una sigla di 2 lettere (per esempio, UJ). Oltre questa sigla vengono riportati i numeri che identificano il punto, messi in sequenza esting-northing; per esempio 32TUJ70821529 indica un punto, con la precisione di 10 m, nella zona 32T, quadrato UJ coordinata Est 7082 e Nord 1529.
- Le due coordinate est/nord devono essere espresse con la stessa precisione (per poterle distinguere), codificata nel seguente modo:
- 1 numero per coordinata: precisione di 10 km: nell’esempio sopra, 32TUJ71;
- 2 numeri per coordinata: precisione di 1 km: nell’esempio sopra, 32TUJ7115;
- 3 numeri per coordinata: precisione di 100 m: nell’esempio sopra, 32TUJ708152;
- 4 numeri per coordinata: precisione di 10 m: nell’esempio sopra, 32TUJ70821529;
- 5 numeri per coordinata: precisione di 1 m: nell’esempio sopra, 32TUJ7082315291.
In Europa la proiezione UTM viene raccomandata da European Spatial Data Infrastructure (ESDI) / Joint Research Center (JRC) per mappatura a scala locale (maggiori di 1:500000), con datum ETRS89 (ETRS-TMzn).
- In Italia è stato utilizzato in Italia con due datum diversi:
- Datum ED50 (European Datum 1950), che utilizza l’ellissoide internazionale, orientato a Postdam. Sono individuati 3 fusi (32, 33 e 34) di 6°. La falsa origine è di 500 km ad est e il fattore di scala è di 0,9996 (vedi Gauss-Boaga). La sovrapposizione tra fusi è di 30”. È utilizzato per la compensazione delle reti geodetiche europee.
- WGS84, utilizzato con i dati GPS e la rete geodetica IGM95. Ha le stesse caratteristiche del datum ED50 (falsa origine, fattore di scala), ma utilizza il datum WGS84.

Come il reticolo Gauss-Boaga, anche per l’UTM il nord del reticolo non coincide con il nord geografico. Nelle tavolette IGM (1:25.000) viene riportata graficamente la differenza tra nord del reticolato e nord geografico (detta convergenza,  ) e tra nord geografico e nord magnetico (detta declinazione magnetica,
) e tra nord geografico e nord magnetico (detta declinazione magnetica,  ), riferite al centro della tavoletta:
), riferite al centro della tavoletta:

ETRS89 / ETRS2000¶
Sistema di riferimento europeo basato su un ellissoide geocentrico, collegato al riferimento geodetico globale (datum) ITRS. Come il WGS84 è basato sull’ellissoide GRS80.
Dovrebbe essere il datum di riferimento europeo per i geodata. Questo sistema deve essere aggiornato (per misure di precisione) ogni 20 anni, per adeguarsi allo spostamento di circa 40 cm (2 cm all’anno verso nord-est per la placca eurasiatica, rispetto al sistema internazionale ITRS) delle placce continentali a causa della tettonica a zolle. ETRS89 è stato aggiornato, nel 2010, con ETRS2000 (che prende come l’2008 come riferimento).
Come sistema cartografico di riferimento per l’ETRS2000 si usa l’UTM.
- (EPSG: 25832): +proj=utm +zone=32 +ellps=GRS80 +towgs84=0,0,0,0,0,0,0 +units=m +no_defs - ETRS89 / UTM zone 32N
In Italia tutte le coordinate della RDN (Rete Dinamica Nazionale) di riferimento per il DGPS (Gps differenziale) sono state ricalcolate in base all’ETRS2000.
Conica di Lambert¶
- La proiezione conica di Lambert è stata raccomandata da European Spatial Data Infrastructure (ESDI) / Joint Research Center (JRC) per la rappresentazione a livello europeo delle informazioni geografiche. Il datum raccomandato è l’ETRS89 (basato sull’ellissoide GRS80 o New International), con le seguenti indicazioni:
- Proiezione equivalente azimutale di Lambert [ETRSLAEA] per la rappresentazione dei dati statistici;
- Proiezione conica conforme di Lambert [ETRS-LCC] per le mappe a scala minore o uguale a 1:500.000;
La proiezione equivalente va utilizzata quando è importante mettere a confronto le aree, in quanto la distorsione nella grandezza degli oggetti rappresentati è minore. Viceversa, quando serve avere meno distorsione sulle forme degli oggetti, conviene utilizzare la proiezione conica.
- La proiezione equivalente richiede 4 parametri:
- latitudine di origine: 52° N
- longitudine di origine: 10° E
- falso nord: 3210000
- falso est: 4321000
- (EPSG: 3035): +proj=laea +lat_0=52 +lon_0=10 +x_0=4321000 +y_0=3210000 +ellps=GRS80 +towgs84=0,0,0,0,0,0,0 +units=m +no_defs - ETRS89 / ETRS-LAEA

- La proiezione conica richiede 6 parametri (2 paralleli standard):
- latitudine di origine: 52° N
- parallelo inferiore: 35° N
- parallelo superiore: 65° N
- longitudine di origine: 10° E
- falso nord: 4000000
- falso est: 2800000
- (EPSG: 3034): +proj=lcc +lat_1=35 +lat_2=65 +lat_0=52 +lon_0=10 +x_0=4000000 +y_0=2800000 +ellps=GRS80 +towgs84=0,0,0,0,0,0,0 +units=m +no_defs - ETRS89 / ETRS-LCC

Gauss-Boaga¶
Il sistema Gauss-Boaga si basa su una proiezione cilindrica trasversa, secante lungo due meridiani. È detta anche Gauss-Kruger, nei paesi tedeschi. In Italia è stata proposta nel 1940 da Boaga. Caratteristica della proiezione di Gauss è l’utilizzo di fusi di ampiezza di 6° di longitudine, un fattore di scala (0,9996) derivato dall’impiego di un cilindro secante la superficie di proiezione, la falsa origine delle coordinate piane, la convergenza dei meridiani ai poli.
Il fattore di scala (0,9996) equivale a trasformare la proiezione cilindrica da tangente a secante. In una proiezione cilindrica tangente, il fattore di scala è 1 solo al meridiano tangente, mentre aumenta allontanandosi. Applicando un fattore di contrazione di 0,9996 viene «rimpicciolito» il cilindro della proeizione, che pertanto diventa secante. L’assensa di distorsione (fattore di scala pari a 1) viene a trovarsi in due meridiani (a circa 2° dal meridiano centrale), corrispondenti alle linee di secanza; il fattore di scala si riduce avvicinandosi al meridiano centrale ed aumenta allontanandosi dai meridiani di secanza. Ne risulta una deformazione media migliore, rispetto al proiezione cilindrica tangente.
- In pratica, a fronte di una lunghezza di superficie terrestre di 1 m, la proiezione porterà ad avere la lunghezza del segmento (rapporto in scala):
- nella cilindrica secante: di 1 m lungo i meridiani di secanza, 0,9996 al meridiano centrale e 1,0004 ai margini del fuso;
- nella cilindrica tangente: di 1 m al meridiano centrale e 1,0008 ai margini del fuso.

Il datum geodetico di riferimento è Roma 1940, che utilizza l’ellissoide internazionale (o di Hayford), orientato a Monte Mario, Roma ( = 41
= 41 ° 55 ' 25 ".51  = 12
= 12 ° 27 ' 08 ".40).
- L’Italia è divisa in due fusi (Est e Ovest) di ampiezza di circa 6
°30', con 30'di sovrapposizione, dovuta all’estensione del fuso ovest di 30': - fuso ovest (fuso 1): da 6
°a 12° 27'08",4, con meridiano centrale posto a 9°ad Est di Greenwich (EPSG: 3003); - fuso est (fuso 2): da 11
°57'08",4 a 18°30', con meridiano centrale posto a 15°ad Est di Greenwich (EPSG: 3004).
- fuso ovest (fuso 1): da 6
- (EPSG: 3003): +proj=tmerc +lat_0=0 +lon_0=9 +k=0.9996 +x_0=1500000 +y_0=0 +ellps=intl +towgs84=-104.1,-49.1,-9.9,0.971,-2.917,0.714,-11.68 +units=m +no_defs - Monte Mario / Italy zone 1
- (EPSG: 3004): +proj=tmerc +lat_0=0 +lon_0=15 +k=0.9996 +x_0=2520000 +y_0=0 +ellps=intl +towgs84=-104.1,-49.1,-9.9,0.971,-2.917,0.714,-11.68 +units=m +no_defs - Monte Mario / Italy zone 2
La zona compresa tra le longitudini –0 ° 30 ' e 0 ° da Monte Mario (11 ° 57 ' 8 ",4 e 12 ° 27 ' 8 ",4 da Greenwich) è una zona di sovrapposizione tra i due fusi ed in essa le coordinate dei punti vengono determinate in entrambi i fusi.

- La falsa origine è diversa per i due fusi:
- 1.500.000 m alla coordinata x (easting) per il fuso ovest
- 2.520.000 m alla coordinata x (easting) per il fuso est (vengono aggiunti 20 km per comprendere una parte del Salento che va oltre la longitudine 18
°30').
- In tal modo la prima cifra della coordinata Est corrisponde sempre al numero del fuso:
- 1 per il fuso Ovest
- 2 per il fuso Est
La convergenza dei meridiani (che, eccetto quello centrale, sono archi e non rette) comporta che il nord della proiezione non indica il nord geografico (salvo al meridiano centrale). In pratica, il nord del reticolo non coincide con il nord geografico (sempre ad eccezione del meridiano centrale), in quanto il reticolato geografico e quello cartografico non coincidono.
- Ne consegue che:
- due punti alla stessa latitudine (A e B) non hanno necessariamente la stessa coordinata (proiettata) Nord;
- due punti alla stessa longitudine (C e D) non hanno necessariamente al stessa coordinata (proiettata) Est.

Cartografia catastale¶
- Le mappe catastali riflettono la frammentazione italiana, in quanto molte derivano (e non sono state aggiornate) dalla situazione pre-unitaria:
- Per alcune aree dell’Emilia-Romagna e Toscana (Modena, Reggio Emilia, Massa-Carrara) viene utilizzato il sistema Sanson-Flamsteed (pre 1886), con circa 150 sistemi locali;
- per lacune aree lombarde (Bergamo, Brescia, Como, Lecco, Varese) il catasto si basava sulla tavoletta pretoriana, senza triangolazione e con nord locale ottenuto con la bussola (Catasto del Lombardo-Veneto);
- Dal 1886 ai primi anni del 1900, sono stati utilizzati oltre 800 sistemi di assi di piccola estensione (piccole origini), con la produzione di più di 100.000 fogli di mappa;
- Dai primi anni del 1900, si sono cominciati ad utilizzare 32 sistemi di assi di grande estensione (grandi origini, in grado di comprendere intere province e in alcuni casi intere regioni), con la produzione di circa 187.000 fogli di mappa.
Dal 1941 la rappresentazione ufficiale è la Gauss-Boaga, per cui si sono dovute trovare opportune trasformazioni per passare dai sistemi cartografici precendenti al nuovo, in particolare al datum Monte Mario 1940.
La proiezione di Cassini è una cilindrica afilattica, ricavata da una cilindrica inversa; è stata modificata da Soldner e adottata per il sistema catastale italiano.

La proiezione di Cassini-Soldner presenta una deformazione lineare massima, entro un raggio di 70 km, dello 0,006 (percentuale) nella direzione del meridiano e nulla in quella del parallelo. Negli ambiti in cui è utilizzata è praticamente equivalente: questo è il motivo per cui è usata per le mappe catastali.
- Il sistema Cassini-Soldner utilizza l’ellissoide di Bessel, orientato:
- a Genova – Monte Telegrafo per il nord Italia;
- a Roma Monte Mario per il centro;
- a Messina – Castanea delle Furie per il sud.
Le mappe catastali fanno riferimento a 32 grandi origini, che fanno riferimento ai 3 centri di emanazione (Genova, Monte Mario, Castanea delle Furie).
Non esiste codice EPSG per questi sistemi di riferimento delle coordinate; la trasformaione deve essere impostata con SR personalizzati.




